衡量一种理论的科学地位的标准是它的可证伪性或可检验性。 – 卡尔·波普尔

前言

昨天在北京，和CodeLab的两个志愿者沟通完之后，一看时间，距离飞机起飞还早。看了下地图，发现当前位置离北大不远，于是准备过去找@yuhao喝个下午茶，扯扯近况吐吐槽。

后来接到@zichun信息说，系统的网络问题解决了，问是否有时间去实验室一趟，于是我就往北邮去了，跟@yuhao没碰上面。

想起来上次和@yuhao在南京碰面，夜里找遍南京的角落，也没找到好吃的馄炖店(@yuhao是南京人，是南京几家馄炖店的铁粉)。找夜宵的路上聊了很多有趣的话题，其中一个是三门问题。我记得我们当时观念分歧，谁也说服不了谁，最终沦为观念之争，因为没法做一万次实验来检验它。于是我上飞机前发信息给@yuhao说，还记得上次在南京吃夜宵聊的门后有羊的概率问题吗？我想到检验这个问题的方法了。

在飞行途中，写了个简单的程序来模拟这个游戏。源码稍后放出，我们从问题说起。

三门问题

我最早听到三门问题好像是在概率论课上，我挺喜欢这门课的，觉得概率论有时触及世界观，关于你如何看待外部物理世界。

三门问题又叫Monty Hall problem，来自于美国的一档电视节目:Let’s Make a Deal, 由于Monty Hall是节目的主持人，于是这个问题得名Monty Hall problem。

这个问题最初是由Steve Selvin在1975年给美国统计学家的一封信中提出的。

三门问题可以表述为:

假设你正在参加一档游戏节目，有三个门供你选择: 一扇门后面是一辆汽车; 其他两扇门的后边是山羊。你的目标是选中汽车。你选择了其中一扇门，比如说1号门。主持人知道三扇门的后边分别是什么。于是他打开了另一扇门(比如3号门)，你看到那里有一只山羊。接着主持人对你说：“你要换选2号门吗？”

那么问题来了，换一扇门对你有利吗？

观念之争

对这个问题，有3种意见在人群中比较典型。

意见一认为换不换无所谓，胜率都是1/3，在游戏开始，每个选项胜率是1/3。主持人排除余下两个选项中的一个错误选项之后，物理世界中没有任何事物发生变化，和初始状态完全相同。所以胜率还是1/3。 无论如何，剩下的两个选项中，肯定有一个是错的，主持人只是帮你指出来，这又没改变什么。

意义二认为应该换2号门。意见二认为在游戏开始时，所做出的选择胜率为1/3。换了2号门之后，等同于一开始同时选择了3号门和2号门，所以胜率变为2/3。

意见三也认为换不换无所谓，但意见三认为，换不换的胜率都是1/2，而不是1/3, 因为主持人帮你排除了一个错误选项，于是问题被重置，成为2选一的问题。

在南京聊到这个问题时，@yuhao持意见三，我持意见二。

争论背后

相较于正确答案是什么，答案所依赖的思考逻辑更有意思。它取决于我们如何看待信息。

这个问题触及信息与现实的关系。

程序模拟

我来给出程序模拟，看看检验的结果如何。思路是通过多次实验，计算频率来估计概率。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58

import random

user1 = "yuhao"  # 坚定不移, 打死不换答案，反正都胜率一样
user2 = "wenjie"  # 摇摆不定, 看到有新的补充信息，就动摇了，还是换吧

def make_a_choice(user):
    choices = ["car", "goat", "goat"]
    # 参与者随机作出一个选择
    user_choice = random.choice(choices)
    choices.remove(user_choice)
    # choices此时为剩余的两个选项
    assert len(choices) == 2
    if user == user1:
        # 第一类用户， 不换答案
        pass
    if user == user2:
        # 第二类用户, 换答案
        '''
        # 模拟主持人的认知过程，掀开门看下是啥，直到看到是羊才展示
        while True:
            remove_choice = random.choice(choices)
            if remove_choice == "goat":
                remove_choice = choices.remove(remove_choice)
                break
        '''
        if choices[0] == 'goat':
            choices.remove(choices[0])
        else:
            choices.remove(choices[1])
        # 主持人排除完错误选项之后，只余下一个选项
        assert len(choices) == 1
        # 参与者选择换选项
        user_choice = choices[0]

    if user_choice == "car":
        is_car = True
    else:
        is_car = False
    return is_car

def game(user, times):
    score = 0 # 得分
    for i in range(times):
        is_car = make_a_choice(user) # 反复进行多个回合，重复实验
        if is_car:
            score += 1
    return score


if __name__ == "__main__":
    times = 100000
    for user in [user1, user2]:
        print(f"game start, user: {user}")
        score = game(user=user, times=times)
        frequency = score / times
        print("game end")
        print(f"user: {user}, times:{times}, score: {score}, score/times: {frequency}")
        print("#"*20)

程序非常简单。

运行的结果为:

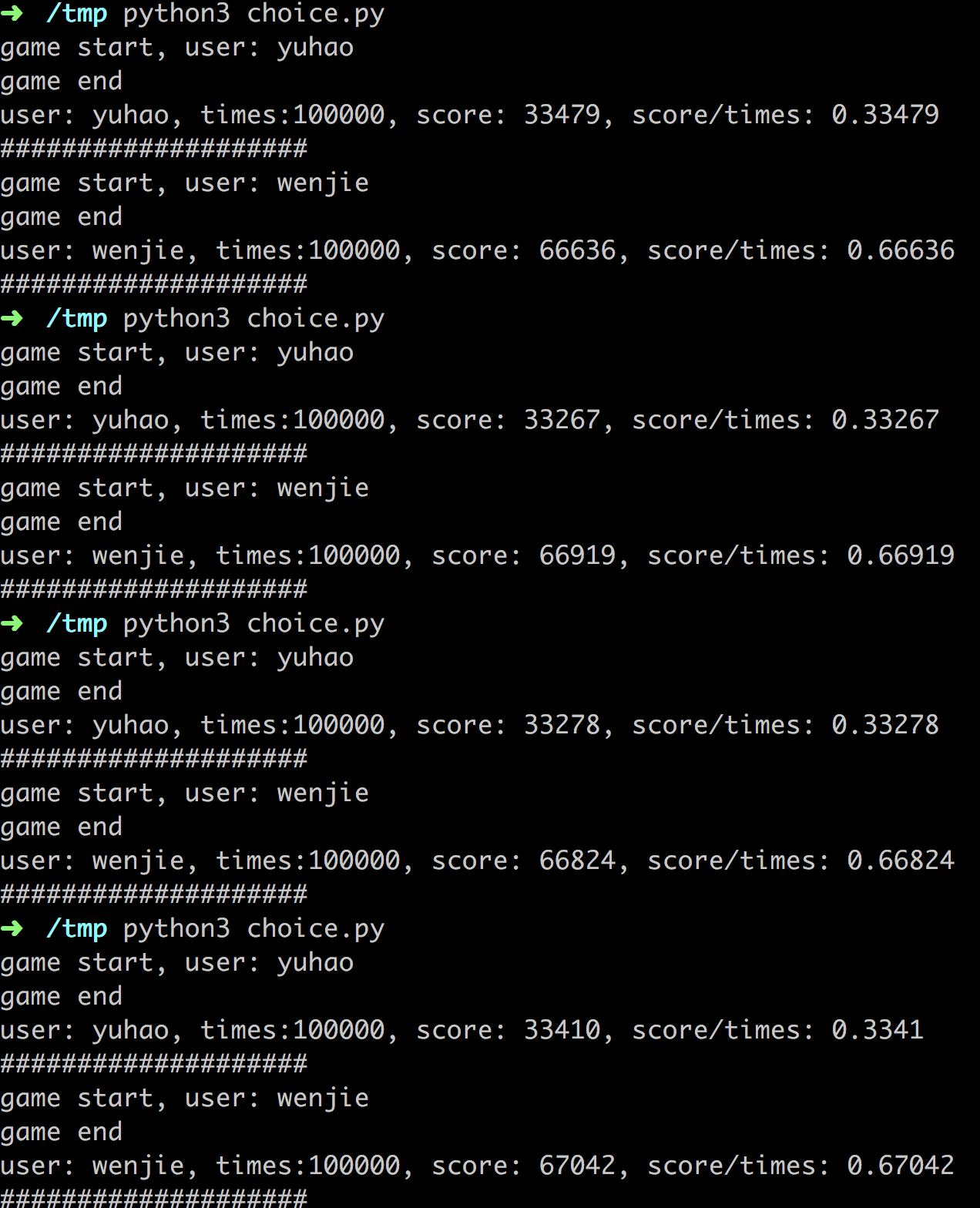
我总共做了4组实验，每组包含有100000次(10万次)模拟游戏。

结论是: 选择换选项的胜率稳定在2/3, 选择不换的胜率稳定在1/3。尽管每次实验，略有差异，但在统计上基本稳定。

程序中有没有可以质疑的地方呢？我觉得是有的。

猜想与反驳

随机数

我们知道计算机的随机数并不是真的随机，是不是计算机产生随机数的机制有偏见，如果产生随机数的机制依据了统计学公式，那么产生的随机数一定满足统计学规律。

我们来试着排除这个影响。

1
2

choices = ["car", "goat", "goat"]
user_choice = random.choice(choices)

这两行模拟了参与者的随机决策。怀疑论者会问，我们怎么知道random.choice(choices)在选择的时候，不会与"car"在choices中的位置相关，毕竟我们不知道这里随机背后规则是什么。通过调整"car"的次序可以回答这个问题，位置对结果没有影响。

怀疑论者会继续问，我们怎么知道random.choice会不会偏好更长的字符串。这个问题其实也很容易做实验解决。

怀疑论者常常能把我们带到远处。更有趣的问法是，我们知道计算机的随机数并不是随机产生的，所以它的统计学规律内在于它的产生机制中。我们会类比说，现实世界之所以出现稳定的统计规律，这种现象是不是揭示了宇宙里有某种硬编码的规则。

统计规律的背后是空无一物还是有所支撑，这个问题完全变成形而上学问题了，多说无益。

主持人的决策

代码里还有一处值得关注。

主持人是如何帮我们排除一个错误选项的呢？

如果我们采用日常语言来描述主持人帮我们排除一个错误选项这件事，我们会错过一个有趣的细节，这个细节我是在编程中才发现的。

主持人帮我们排除一个错误选项听起来不需要被特别关注，因为主持人知道什么是错误选项啊，所以他指出来就好了啊。当我们用日常语言表述这句话时，不会在此发生停留，因为它如此自明。

当我们需要在程序中模拟主持人排除错误选项时，代码逼着我们使用明确的逻辑规则来描述。我给出了两个方案都能做到排除一个错误选项，但注意它们是有区别的。

1
2
3
4
5
6

        # 模拟主持人的认知过程，掀开门看下是啥，直到看到是羊才向选手展示
        while True:
            remove_choice = random.choice(choices)
            if remove_choice == "goat":
                choices.remove(remove_choice)
                break

这个方案让主持人随机打开一个门，当看到山羊就指出来。

1
2
3
4

        if choices[0] == 'goat':
            choices.remove(choices[0])
        else:
            choices.remove(choices[1])

这个方案似乎是有序的，主持人从左到右，或从右到左开门，查看物体是不是山羊。

从代码中你会近距离注意到，主持人的认知和操作过程。我们看到主持人为了找出山羊在哪里，他认真检查了选项，有时候检查了2个选项, 自然语言中我们很难注意到这点。如果你在编程的时候，把主持人想象成选手，你发现他有两次机会做选择! 所以我们当然采用主持人的选项！

后话

@yuhao是凝固态物理博士，对量子力学了解很多，之前送了我一本书叫《不同的宇宙》，这本书机智幽默，罗伯特·劳克林在书里讨论物理学中还原论和涌现理论的分歧，也讨论一些有趣的量子力学问题，我非常喜欢这门书，它在带着我们思考，而不是罗列定律。

我有个奇怪的感觉，概率论的有效性可能揭示出物理世界的某种逻辑结构，这个结构受信息的影响，而不只是受物质和能量的影响。

但概率论只是指出，而没有作出解释。

为什么是这组而不是另一组统计规律？为何是这一簇而不是另一簇物理规律？

物理世界是不是一种模拟？

@yuhao说别纠结这个，它既不可证实也不可证伪，只会带来观念之争。

我并不纠结，但我饶有兴致。我不害怕它是模拟，柏拉图、卢梭、黑格尔才害怕，因为现实一旦是模拟，他们那些残酷又严肃的理论就显得极为可笑, 他们把意义建立在个人之外,他们把意义建立在强权之上。

我们拥抱所爱之人，热爱自由和平等，对他人的苦难感同身受，这些不会因为这个世界是模拟而有损于生命的意义。

但物理世界如果是模拟，这是多大的乐趣啊，我们就可能hack它。

参考