递归问题

为了理解递归，必须首先理解递归。

前言

近期开始讲授两门编程入门课:

其一在汇景创造乐园, 关于 Python 入门。
其二在实务学堂，web 职业方向。

上周五晚上在汇景开始第一次授课。

以下是我的围绕第一次课《编程是什么?》制作的讲稿（Google Slides）: 编程是什么?

课程的参与者中，@weiran 有编程经验（在编程比赛中拿过金奖）。之前与 @weiran 父亲认识，此次 @weiran 带着一些问题来听课，课后与我讨论了一些困扰他已久的递归问题，觉得递归的概念难以理解。

我给他分享了两份材料:

SICP Python 描述
The Little Schemer

递归，在数学与计算机科学中，是指在函数的定义中使用函数自身的方法。递归一词还较常用于描述以自相似方法重复事物的过程。 – 维基百科

正式定义: 在数学和计算机科学中，递归指由一种（或多种）简单的基本情况定义的一类对象或方法，并规定其他所有情况都能被还原为其基本情况。 – 维基百科

递归是一种信仰

LISP 是一门宗教，递归是一种信仰

我们先来看看《SICP Python描述》对递归的精彩讨论。

将递归调用看做函数抽象叫做递归的“信仰飞跃”(leap of faith)。我们以函数自身来定义函数，但是仅仅相信更简单的情况在验证函数正确性时会正常工作。 –《SICP Python 描述》

这可能是关于如何把握递归，最精彩的描述之一。

以阶乘的递归描述为例:

1
2
3
4


def fact(n): 
    if n==1:
        return 1
    return n * fact(n-1)

这个例子中我们相信 fact(n-1) 会正确计算 (n-1)! ，然后把 fact(n-1) 当作一个抽象函数(黑盒)即可，而不要试图展开去理解它！

为了理解递归，你必须信任递归函数会完成它的目标。

几道问题

语言并不是你学到的东西，而是你参与的东西。 – Arika Okrent

我讨厌解题，就像讨厌写命题作文。

编程是关于我想让计算机做什么，而不是我要掌握的技巧，除非那些技巧跟我想做的事情有关。

所以 @weiran 给我发的几个递归题目，我没细看。相比于解几道递归题目，更重要的是理解递归想法本身的力量，而理解递归的力量，再在没有比 LISP 社区更为深刻的了，所以我跟他简单聊了LISP社区对递归的看法（受到Alan Kay、Paul Graham、SICP和LISP 1.5手册的影响），分享了一些资料。

周末有空，把 @weiran 发给我的几个问题仔细看了下，似乎还挺好玩，一种脑筋急转弯的乐趣, 聊作消遣。

问题 1

我们先以一道有答案的题目为例:

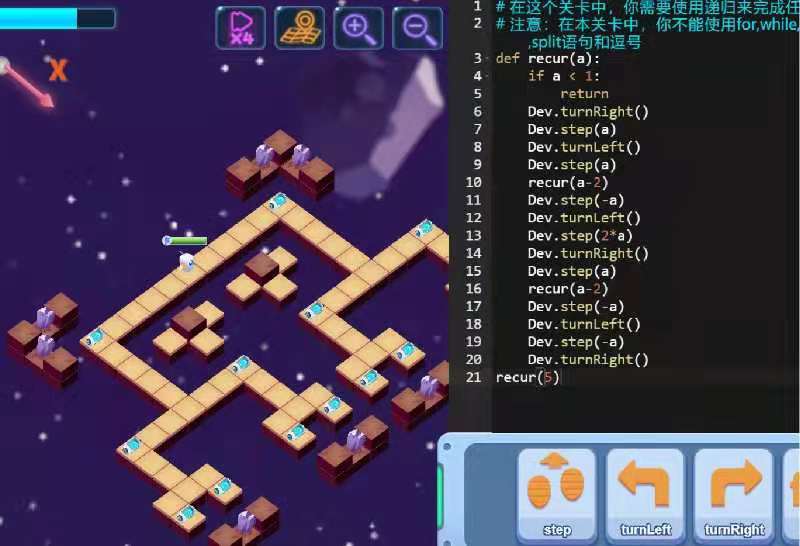
这题目看起来是要采集到所有的蓝色能量块/宝石。

不知道这是什么编程平台，准备用 Python turtle 模拟它: 走路采集宝石和 turtle 走路画出某种路径图案(宝石在路径上)是等效问题。

写了个简单模拟器（使用Mu editor）:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14


import turtle

t = turtle.Turtle()
t.speed(1) # 慢速移动

def step(x):
    ONE_STEP = 20 # 步长
    t.forward(ONE_STEP * x)

def turnRight():
    t.right(90)

def turnLeft():
    t.left(90)

接下来，我们来走出这个递归图案

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33


def recur(a):

    # 结束条件
    if a<1:
        return

    # 前往第1个递归位置
    turnRight()
    step(a)
    turnLeft()
    step(a)

    # 抵达第1个递归位置
    recur(a-2)  # 画出下一个图案，相信这个函数会画出，别管它怎么画出

    # 前往第2个递归位置
    step(-a)
    turnLeft()
    step(2*a)
    turnRight()
    step(a)

    # 抵达第2个递归位置
    recur(a-2)  # 画出下一个图案

    # 回到出始位置
    step(-a)
    turnLeft()
    step(-a)
    turnRight()

t.right(45) # 初始朝向
recur(5)

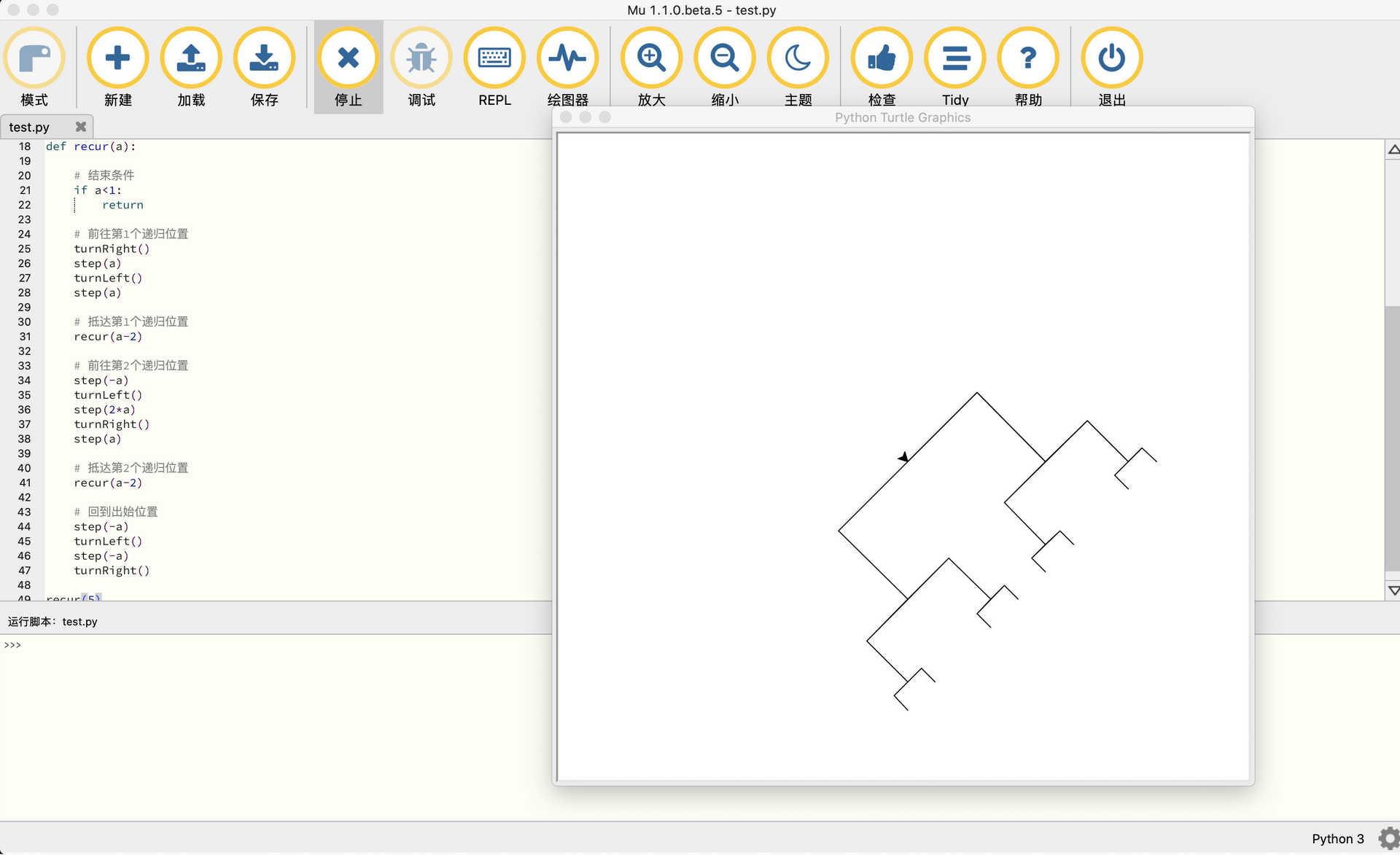
初次接触递归的小伙伴，可能会试图在每个 recur(recursion) 函数里展开 recur 函数，大脑内存一下就不够用了。

思考方式

思考递归的关键是相信递归函数会完成它的目标。

观察上边的结构。

我们发现上边蓝线标注的图案，反复出现（递归），我们把它下一次出现的位置(绿色星星)称为递归位置，只需要关注子代的递归位置即可，别去管太远的后代。

开始定义递归函数: recur(你可以把它叫做 画出蓝线图案，接受一个参数: 走几步)，重点是相信递归函数会完成它的目标，然后，抽象地使用它（关注语义，而不是实现）。

总结来说, 定义一个递归函数，在函数内做一下几件事:

确定递归位置(当前题目有左右两个递归位置)
依次前往递归位置（在每个递归位置，确认与初始状态（朝向）一致）
调用递归函数，画出下一个递归图案（相信递归函数会画出蓝线，只是参数不同）
回到初始位置（确保姿态和初始状态一致）
注意结束条件.

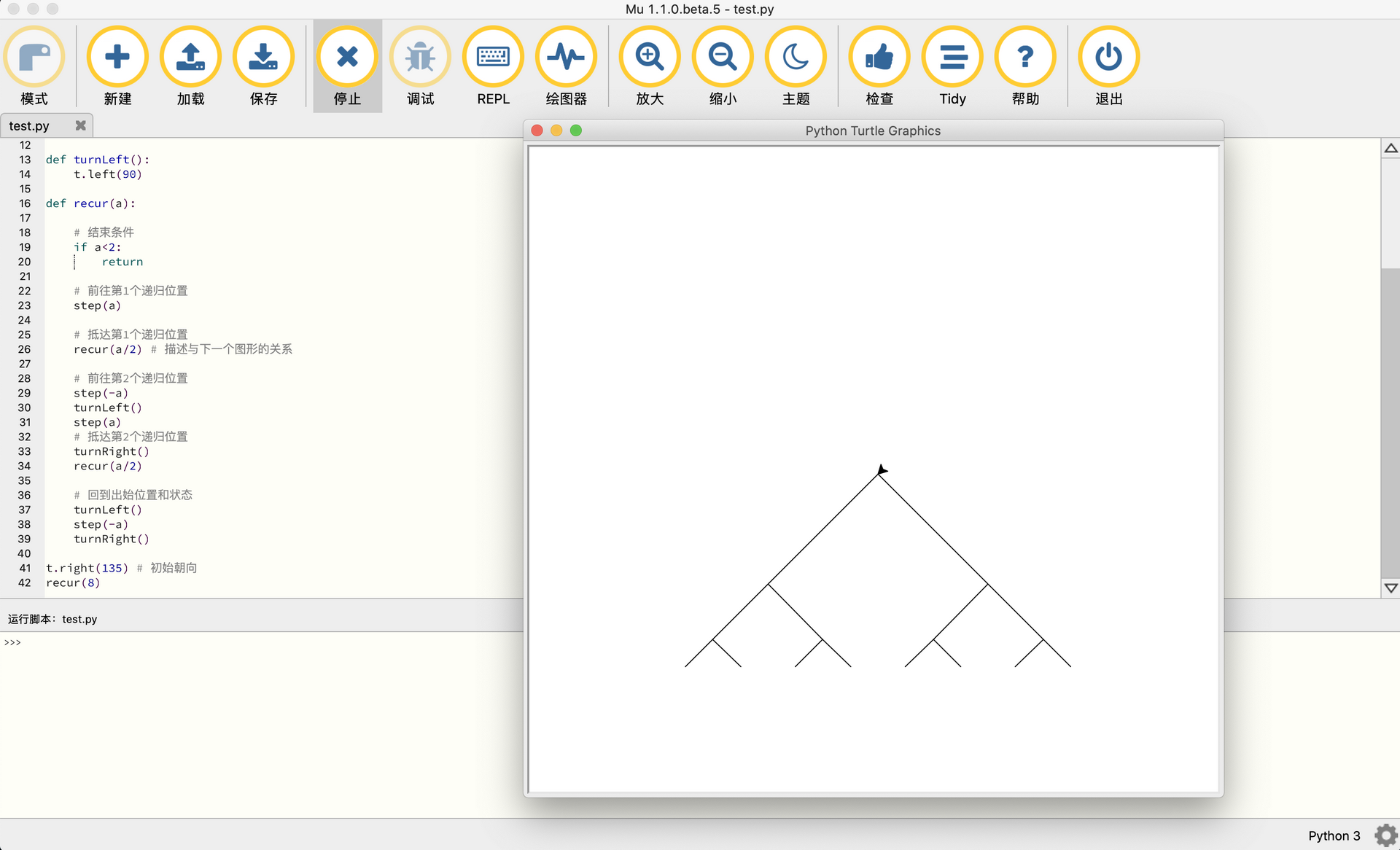
在另一道题上试试我们的方法:

首先我们观察到递归绘制的图形是:

然后开始写代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27


def recur(a):

    # 结束条件
    if a<2:
        return

    # 前往第1个递归位置
    step(a)

    # 抵达第1个递归位置
    recur(a/2) # 描述与下一个图形的关系

    # 前往第2个递归位置
    step(-a)
    turnLeft()
    step(a)
    # 抵达第2个递归位置
    turnRight()
    recur(a/2)

    # 回到出始位置和状态
    turnLeft()
    step(-a)
    turnRight()

t.right(135) # 初始朝向
recur(8)

其他练习题

大家有兴趣可以试试其他练习题:

小结

通过以上这类递归题目: 在空间里走出目标路径(等效于绘制几何图形)，我们分享了思考递归的一些有力方式。

递归的趣味和力量远不止如此。

如果你只是把递归看作一种解题技巧，那么你会错失它的真正力量。

试着把它看作看待/描述问题的方式，这是LISP社区一贯以来的视角。

如果你想真正掌握递归的力量，你应该进入 LISP 社区的 context。

如果你是 Python 用户，《SICP Python 描述》是很好的入口，如果你愿意入门 LISP，试试《The Little Schemer》。

一种不会影响你思考编程方式的语言是不值得学习的 – Alan Kay

与递归有关的一些强有力观点(Powerful Ideas)

将代码看做递归数据结构（LISP: S表达式）
将对象看做递归的计算机 (Smalltalk: 对象负责计算)

以上想法为这两门语言带来了晚绑定(late binding)的能力，是它们灵活性的根源之一。

也为这两门语言带来了强大的元能力。

附

关于递归的性能问题以及改进方案，《SICP Python 描述》也有精彩讨论。

文章目录

前言